O que indica uma forma em forma de cunha do gráfico PCA?

No seu papel em autoencoders para classificação texto Hinton e Salakhutdinov demonstrado o lote produzido por 2-dimensional LSA (que está intimamente relacionado com a PCA): .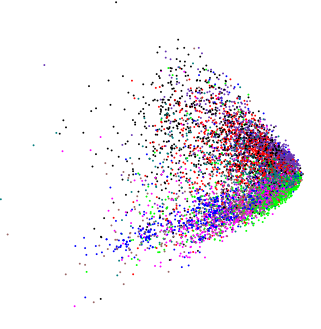

Aplicando o PCA a dados de dimensão ligeiramente alta absolutamente diferentes, obtive um gráfico de aparência semelhante: (exceto neste caso, eu realmente queria saber se existe alguma estrutura interna).

Se alimentarmos dados aleatórios no PCA, obteremos um blob em forma de disco, portanto essa forma em forma de cunha não é aleatória. Isso significa alguma coisa por si só?

Supondo que as variáveis ​​sejam positivas ou não negativas, as bordas da borda são apenas pontos além dos quais os dados se tornariam 0 ou negativos, respectivamente. Como esses dados da vida real tendem a ser distorcidos corretamente, vemos maior densidade de pontos na extremidade inferior de sua distribuição e, portanto, maior densidade no "ponto" da cunha.

De um modo mais geral, o PCA é simplesmente uma rotação dos dados e as restrições nesses dados geralmente serão visíveis nos componentes principais da mesma maneira mostrada na pergunta.

Aqui está um exemplo usando várias variáveis ​​log-normalmente distribuídas:

library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

Dependendo da rotação implícita nos dois primeiros PCs, você poderá ver a cunha ou uma versão um pouco diferente, mostrada aqui em 3d usando ( ordirgl()no lugar de plot())

Aqui, em 3d, vemos vários picos saindo da massa central.

$X_i \sim \mathcal(N)(\mu = 0, \sigma = 1)$

set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")

E para variáveis ​​aleatórias positivas uniformes, vemos um cubo

set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")

Observe que aqui, para ilustração, mostro o uniforme usando apenas 3 variáveis ​​aleatórias, portanto, os pontos descrevem um cubo em 3d. Com dimensões mais altas / mais variáveis, não podemos representar perfeitamente o hipercubo 5d em 3d e, portanto, a forma distinta de "cubo" fica distorcida. Problemas semelhantes afetam os outros exemplos mostrados, mas ainda é fácil ver as restrições nesses exemplos.

Para seus dados, uma transformação de log das variáveis ​​anteriores ao PCA puxaria as caudas e esticaria os dados agrupados, assim como você pode usar essa transformação em uma regressão linear.

Outras formas podem surgir em gráficos de PCA; uma dessas formas é um artefato da representação métrica preservada no PCA e é conhecida como ferradura . Para dados com um gradiente longo ou dominante (as amostras organizadas em uma única dimensão com variáveis ​​aumentando de 0 a um máximo e depois diminuindo novamente a 0 ao longo de partes dos dados são conhecidas por gerar esses artefatos.

ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
                 Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
                 Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
        ylab = "Abundance", xlab = "Sites")

que produz uma ferradura extrema, onde pontos nas extremidades dos eixos se dobram de volta para o meio.