Estou tentando criar uma esfera quadrada com base em um artigo , que mostra resultados como este:
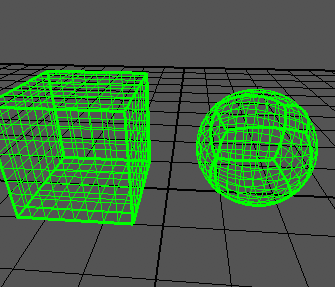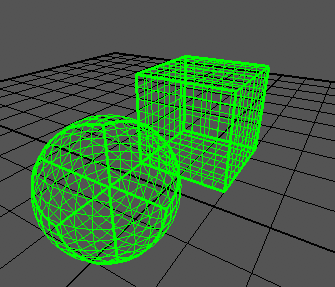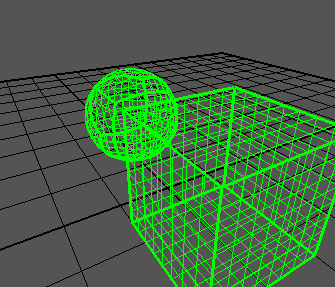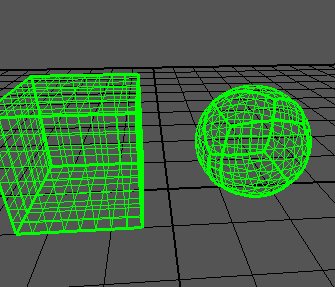
Eu posso gerar um cubo corretamente:

Mas quando eu converter todos os pontos de acordo com esta fórmula (da página vinculada acima):
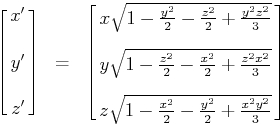
x = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
y = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
z = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));
Minha esfera fica assim:

Como você pode ver, as bordas do cubo ainda se destacam demais. O cubo varia de -1a +1em todos os eixos, como diz o artigo.
Alguma ideia do que está errado?

Respostas:
Você escreveu errado a fórmula.
Você modifica o original
xe o substitui. Então você modifica comybase não no original,xmas no modificadox. Em seguida, você modifica comzbase na versão modificada de ambos .Preserve os originais e calcule:
Use dx, dy e dz a partir de então.
fonte