Conforme Wikipedia , podemos escrever qualquer estado puro como
| ip⟩=cos( θ2) | 0⟩+ eeu ϕpecado( θ2) | 1⟩
Onde e ϕ são os ângulos da esfera de Bloch:θϕ
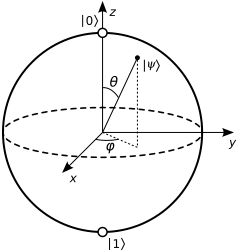
Quase qualquer ponto da superfície (ou seja, estado puro) tem uma representação única em termos de ângulos, exceto os pólos. Assim como na Terra, o Polo Sul não tem longitude bem definida (qualquer longitude funciona da mesma maneira), para o estado qualquer fase φ significa a mesma coisa. A "latitude" θ está aqui π , vamos inserir isso na equação:| 1⟩ϕθπ
=0+ei& Phi;| 1⟩
| 1⟩=cos( π2) | 0⟩+ eeu ϕpecado( π2) | 1⟩=
= 0 + eeu ϕ| 1⟩
Se você estiver familiarizado com a identidade de Euler, você provavelmente irá reconhecer como uma rotação no plano complexo. Em particular, como Z é uma rotação para ϕ = π , obtemos o famoso e i π = - 1 , chegando finalmente a | 1 ⟩ = - | 1 ⟩ .eeu ϕZϕ = πeeu π= - 1| 1⟩=- | 1⟩

